Do you remember when you first started studying in higher classes like 9th and 11th standard? That was obviously a tough time for you and your brain. Everyone experiences that kind of pressure once in their lifetime. There are hundreds of new topics that you only had to listen to name about in junior classes. But when you see them in actual you’ll either find them very tough or very playful. In all those topics there was one topic which is not going to leave your back once you start studying it. This is Function, and here we are going to cover how to tell if a function is an Even or Odd Function?
This is quite easy only if you know the proper methods of identifying a function. So let’s get started with the introduction and some applications of function.
What is Function?
One of the most important concepts in mathematics, Functions are the base of the building blocks of Mathematics. It forms one of the most important pillars in Mathematics, no matter which stream you’re studying in. Functions will always appear in various forms, for instance like integration and differentiation.
The function is actually derived from a Latin word which means operation and word mapping and maps are synonyms to it. If we look for a definition mathematically then, Let A and B be two non-empty sets. The relation f from A to B, i.e. a sub-set of AB, is called a function (or a mapping or a map) from A to B, if
(i) for each aA there exists bB such that (a,b)f.
(ii) (a,b)f and (a,c)fb=c.
What is Even Function and Odd Function?
A function f(x)=xnis said to be an even function when n is an even integer and it is said to an odd function when n is an odd integer. There are various other properties through which a function can be odd and even, and it can be identified easily as well. Some properties for a function to be an even or an odd function are as follows:
- When adding two even functions, the result will also be an even function.
- When subtracting the two odd functions, the result will also be an odd function.
- When adding two odd functions, the result will also be an odd function.
- When subtracting two even functions, the result will also be an even function.
- When multiplying two odd functions, the result will be an even function.
- When multiplying two even functions, the result will be also an even function.
- When multiplying one odd function and one even function, the product will be an odd function.
- When dividing two even functions, the quotient will be an even function.
- When dividing two odd functions, the quotient will be an even function.
- And, when dividing one odd function and one even function, the quotient will be an odd function.
How to tell if a function is An Even or An Odd Function?
All of these above properties will help you identify the evenness and oddness of a function, visually. But there are other two methods through which someone can ask you to determine a function, whether is it odd or even.
The other two methods of determining or identifying a function are Algebraically and Graphically. These two methods are the only used methods in examinations, whether it’s a high school exam or a college exam.
Determine algebraically whether a function is an odd or an even function
If someone asks you to determine a function algebraically, then all you need to do is to simplify the function. It is a very simple trick, after simplifying if your answer is the exact same copy of your initial point, that means where you started, not even the signs are different then this is an even function. But if your answer has even a single difference from your initial point then it will be an odd function.
For instance, if there is a question like this, determine the f(x)=-3×2+4 is even or odd.
You simply put -x for all the values of x, and then do the further simplification:
f(-x)=-3(-x)2+4
=-3(x2)+4
=-3×2+4
Now, we can see that the final result is the exact same copy of the point where we started simplifying the sum. Hence, it is an even function.
And there is another sum which you asked to determine algebraically that whether is an even function or an odd function. The sum is f(x)=2×3-4x. Simplify it:
The same thing we will do for this also, place the value of x as -x.
f(-x)=2(-x)3-4(-x)
=2(-x3)+4x
=-2×3+4x
Hence, here we see that the symbols are changed now after simplifying the sum, so we can say that this function is an odd function.
Graphically Determination
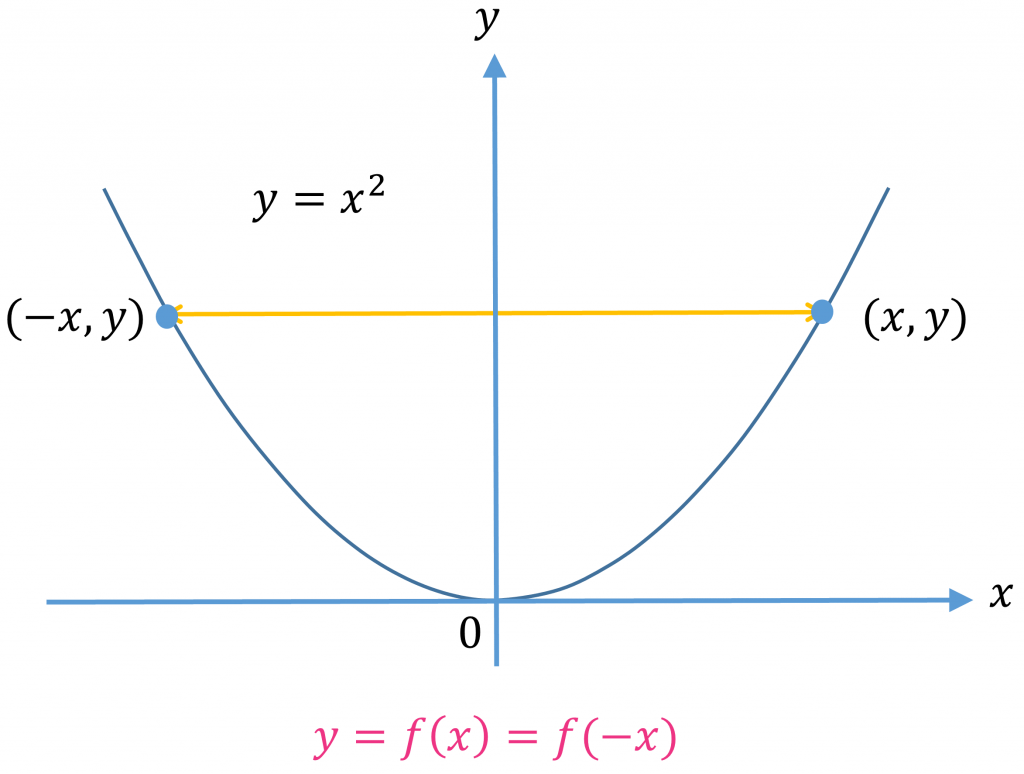
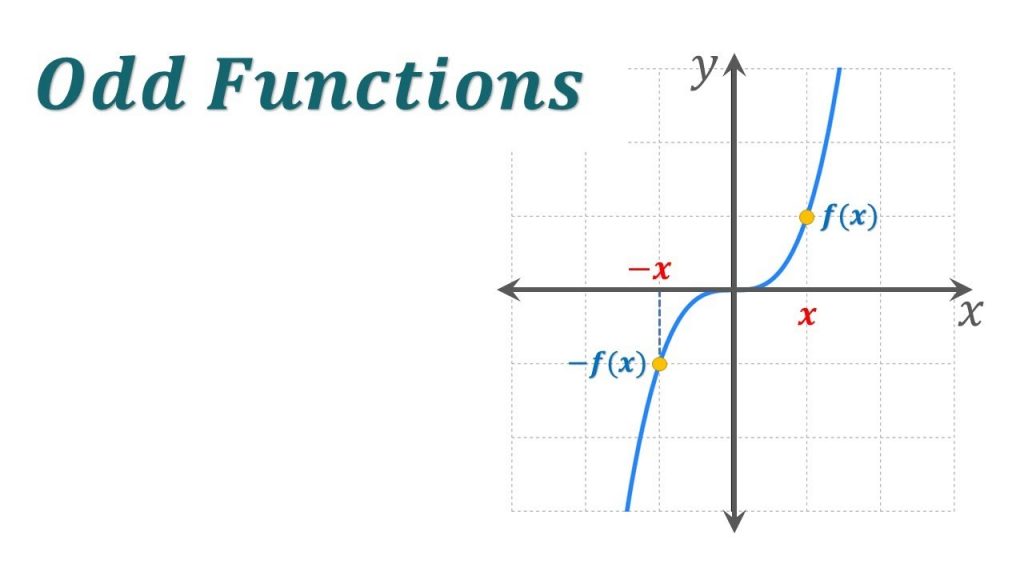
Identifying an Even or Odd Function is way too easy from all of the above methods and properties. All you have to do is to look at the y-axis. If a line is symmetric about the y-axis then it is an even function and when a line is symmetric about the origin, then it is an odd function.



